4.地震
a. 地震の揺れと震源
地震の揺れ
地震動:地震による地面の揺れ
「地震」は地震動を起こす地球内部の現象を指す
揺れの経験
関東地震(1923年9月1日11時58分、M7.9、死者14万人余り)
阿部理学士が震源域のほぼ真上で体験
「最初に縦揺れ。その後の激しい揺れで、
地面に這いつくばって、立つこともできなかった」
地震波の伝播との関係(図:地震波の伝播、P波とS波の波形)
縦揺れと横揺れの存在;P波とS波
震源のごく近くでは、P波とS波が混在
震源からある程度離れた地点で観測
P波やS波の他に、各種の揺れが続くことがある
P波やS波が反射や屈折して届く
主な反射面は、地表、マントル・核境界
表面波;P波やS波より振幅が大きいことが多い
P波が、振幅が大きいS波や表面波に先行
P波を用いて、もっと大きな揺れのくることを警告
ナウキャスト地震情報
Q. ナウキャスト地震情報は、どう活用できるか?
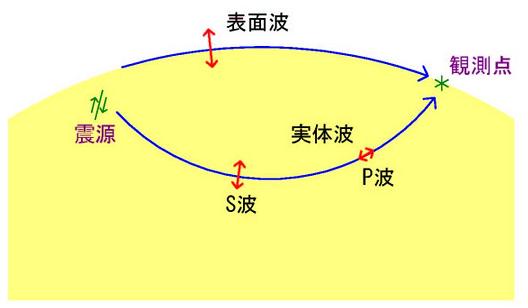
実体波と表面波(図:表面波)
実体波:地球内部を伝わる波。P波(縦波)とS波(横波)
S波の伝播速度は、P波の60%程度の大きさ
表面波:地球の表面に沿って伝わる波
地表付近のみで大きな振動、深さとともに振幅が急減
伝播速度は、S波の90%程度の大きさ
震源が浅いときに、顕著に生ずる
振動のエネルギーが、表面付近に偏るため、減衰が小さく、振幅が大きい
表面波には、レイリー波とラブ波が存在
レイリー波:鉛直方向と伝播方向に振動
ラブ波:伝播方向と垂直な水平方向に振動
深さとともに速度が急増する場所で生じる
下図:G. A. Eiby "Earthquakes"(Heinemann, New Zealand)より
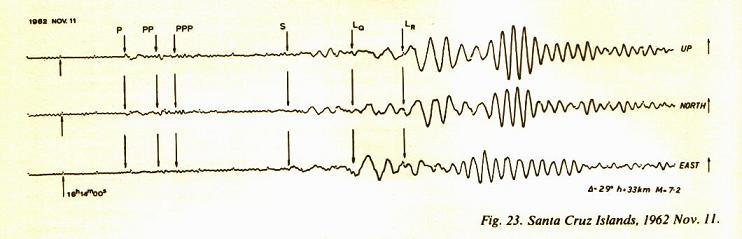
Q. 地震の表面波は水面波とどう違うか?
震度
震度:地震動(地震の揺れ)の大きさを段階で表す
震度計(加速度型地震計、強震計)で測られる計測震度を丸めて10段階で評価
震度は、体感や被害の程度と対応づけられる
震度5弱以上で、建物などに被害
震度6弱以上で、家屋の倒壊が始まる
歴史的には、体感や被害の程度を表現する震度表が最初に作られた
兵庫県南部地震を契機に、気象庁は1996年から震度計を用いることにした
現在、全国に3000箇所以上に震度計が分布
震度データは、地震が起こるとただちに発表
外国では、体感や被害に基づく震度が現在も使われている
定義自体も国により異なる
よく使われるのは、改正メルカリ震度
震度の定義と意味
_____________________________________________________________________________________
震度 計測震度 よく見られる現象
_____________________________________________________________________________________
0 0-0.5 人は揺れを感じない。
1 0.5-1.5 屋内の一部の人がわずかな揺れを感じる。
2 1.5-2.5 屋内では多くの人が揺れを感じ、眠っている人の一部は目を覚ます。吊
り下げた物がわずかに揺れる。
3 2.5-3.5 屋内のほとんどの人が揺れを感じ、恐怖感を覚える人もいる。棚の食器
類が音を立てることがある。
4 3.5-4.5 屋内ではかなりの恐怖感があり、眠っているほとんどが目を覚ます。
座りの悪い置物が倒れる。
5弱 4.5-5.0 棚の食器類や本が落ち、家具が移動することがある。弱い壁に亀裂が
生じることがある。落石や小さな崖崩れが生じることがある。
5強 5.0-5.5 棚の物が多く落ちる。タンスが倒れることがある。補強されていないブ
ロック塀、備え付けの悪い自動販売機、墓石の多くが転倒する。弱い家
屋の破損、耐震性の高い建物に亀裂が生じることがある。
6弱 5.5-6.0 立っていることが難しい。多くの家具が移動、転倒する。弱い住宅は倒
壊するものがあり、鉄筋コンクリート造でも壁や柱に亀裂が生じる。
地割れ、山崩れが生じることがある。
6強 6.0-6.5 立っていることができず、はってしか動けない。家具のほとんどが移動、
転倒する。弱い建物の多くが倒壊し、耐震性の高い建物でも壁や柱が破
壊するものがある。
7 6.5- 人は自分の意志で動けない。ほとんどの家具が大きく移動し、飛ぶもの
もある。耐震性の高い建物でも傾いたり、大きく破壊するものがある。
_____________________________________________________________________________________
Q. 震度の決定に震度計を使う利点をあげよ
震度分布の例
鳥取県西部地震;2000年10月6日、マグニチュード7.3(図)
最大震度6強で、7にならなかった;断層が地表まで達しなかったため
死者0人、重軽傷100人程度、2000戸余りの家屋が全半壊
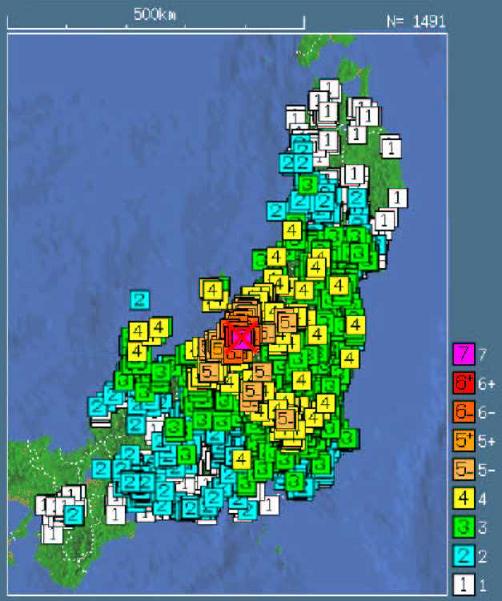
新潟中越地震;2004年10月23日、マグニチュード6.8(図)
断層が地表近くに達したため、最大震度が7になった
死者46人、重軽傷約4800人、3000戸余りの家屋が全壊
下図:気象庁のホームページより
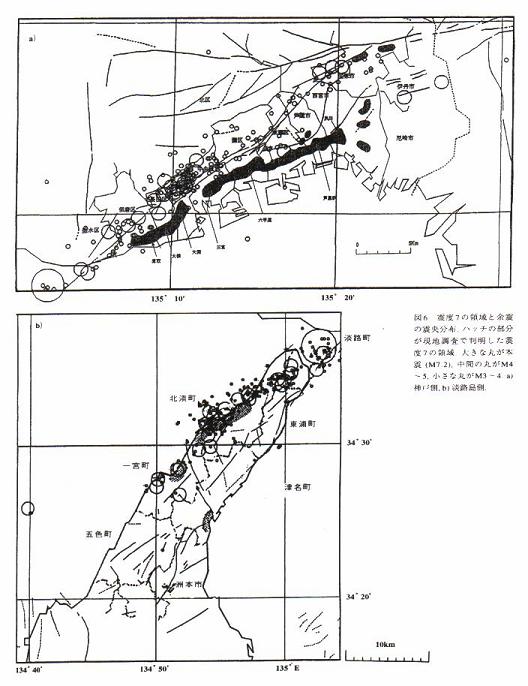
兵庫県南部地震;1995年1月17日、マグニチュード7.2(図)
計測震度を用いる以前の震度;神戸付近で震度6、姫路で震度4
後から調べて、帯状に震度7の分布
死者6400人、重軽傷約4万人、家屋の全壊10万戸、半壊14万戸
下図:気象庁の資料
地震動への地盤の効果
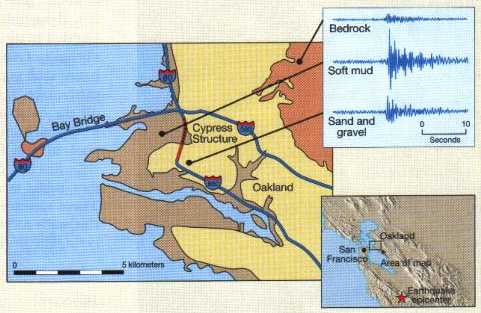
ロマプリータ地震の例(図:地盤による波形の違い)
ロマプリータ地震;M7.1、死者67人
地盤の弱い場所で、高速道路が倒壊した
震源から同じような距離でも、揺れ方が大きく異なる
扇状地などの脆弱な地盤は、揺れが増幅される
周辺との地震波速度の違いで、振動エネルギーがトラップされる効果も
液状化現象:水を含んだ砂地を揺らすと液状化(図:液状化現象)
地面から水が噴出して、泥火山ができる
地盤は液になって流れ、強度を失い、建物などが倒壊
液状化の原因
接触によって支えられた砂粒が、揺れによって支えを失う
砂粒は液体の中に埋没して、全体が流動化
下図:E.J.Tarbuck & F.K.Lutgens "Earth"(Prentice Hall)より
震源の位置の計算
地震波速度が一定な場合
P波とS波の到着時刻の差から、観測点と震源の距離を決める
距離 = 時間差×VpVs/(Vp-Vs)
3点以上の観測点からの距離から、震源の位置が決まる
各観測点から、距離を半径とする球を描き、交点を求める
実際に使われる震源決定(地震波速度の分布は既知とする)
複数の観測点でP波、S波の初動時刻を決める
観測結果が計算結果と合うように、地震の発生時刻と発生位置を同時に決める
発生時刻、発生位置の適当な値からスタートして、地震波の到達時刻を計算
計算結果と観測値のずれを減らすように、発生時刻、発生位置を修正
その操作を収束するまで繰り返す
震源の位置は、震央(震源の真上の点)の位置と深さで表現
Q. 震源は地震の原因となる変動が開始した地点を示す。何故か?
マグニチュード
マグニチュードは、地震の大きさを表現する尺度
震源から地震波として放出されるエネルギーに対応
各々の地震に固有の値で、震度のように場所に依存しない
マグニチュードの決め方
標準的な地震計を用いて、地震記録の最大振幅Aを読み取る
振幅は地震によって何桁も変わるので、その常用対数をとる
遠くに離れるほど振幅は小さくなるから、それを補正する、
マグニチュード M = log A −αlog r rは震央距離、αは定数
よく使われるマグニチュード
実体波マグニチュード:周期数秒のS波の振幅を使う
表面波マグニチュード:周期約20秒の表面波の振幅を使う
これらのマグニチュードは、巨大地震の大きさをうまく表現できない
断層運動に基づいて決めるモーメント・マグニチュードを使う
モーメントは、断層の両側で逆向きに働く「力の対」のこと
地震波として放出されるエネルギー
エネルギー E log E = 1.5M + 定数
マグニチュードが1上がると、エネルギーは30倍になる
エネルギーはモーメントに比例する
Q. 震度とマグニチュードの違いを説明せよ
マグニチュードの例
兵庫県南部地震(1995.1.17):7.2(死者6400人)
鳥取県西部地震(2000.10.6):7.3
新潟中越地震(2004.10.23):6.8(死者46人)
関東大地震(1923.9.1):7.9(死者14万人余り)
南海地震(1946.12.21):8.0(死者1500人)
チリ地震(1960.5.23):9.5(世界で最大級、死者数千人、日本でも津波で139人)
スマトラ島沖地震(2004.12.26):9.3(津波などにより死者30万人)
地震の発生回数(図:地震の頻度とマグニチュード)
地震の頻度(単位時間あたりの発生回数)
地震の発生回数は、地震が大きくなるほど少ない
マグニチュードが1上がると、頻度はほぼ1/10に減る
マグニチュードと頻度の関係
log N = C − bM log n = c − bM ; c = C + log b
N:マグニチュードがM 以上の地震の総数
n:マグニチュードがM −0.5とM +0.5の間にある地震の数
b (b値)はほぼ1に近い数、地震が起こる場所の性質を反映
不均一な場所ほど、bが大きい(小さい地震の数が相対的に多い)
地震が小さくなる程、発生回数が多くなる理由
小さい地震の方が、断層が小さいので、選択しうる場所の数が多い




